Wenn Sie das Wort "Fibonacci" hören, denken Sie wahrscheinlich an Mathematik und nicht an Streetwear-Mode. Aber diese beiden Bereiche haben mehr gemeinsam, als Sie vielleicht denken.
Die Fibonacci-Folge: Eine Einführung
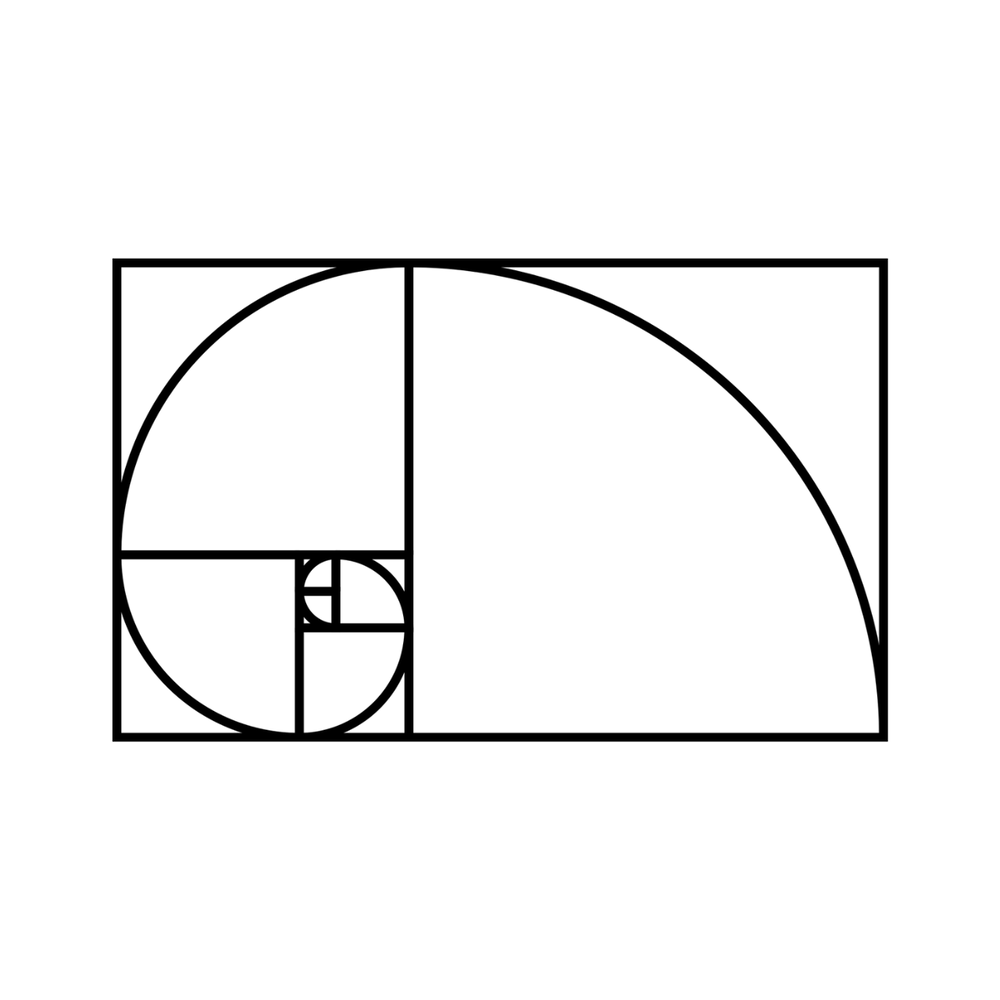
Die Fibonacci-Folge ist eine Zahlenreihe, bei der jede Zahl die Summe der beiden vorhergehenden Zahlen ist: 0, 1, 1, 2, 3, 5, 8, 13 und so weiter. Diese Sequenz führt uns zum "Goldenen Schnitt" oder "Goldenen Verhältnis", einer Proportion, die in der Natur, Kunst und Architektur häufig vorkommt.
Das Goldene Verhältnis in der Ästhetik
Aber was hat das Goldene Verhältnis mit Streetwear-Mode zu tun? Das goldene Verhältnis gilt seit der Antike als besonders ästhetisch und findet auch in der modernen Mode Anwendung.
Ästhetik und Proportionen
Das Spielen mit Proportionen kann einen Streetwear-Look aufwerten oder ganz verändern. Ein T-Shirt, dessen Länge und Breite im goldenen Verhältnis zueinander stehen, kann auf das Auge ansprechender wirken. Das gleiche gilt für die Platzierung von Designs oder Logos auf Kleidungsstücken.
Exklusivität und Einzigartigkeit durch Fibonacci
Die Fibonacci-Sequenz ist nicht nur faszinierend, sondern auch mysteriös.
Mehr als nur Stoff und Faden
Ein Design, das die Fibonacci-Sequenz nutzt, kann ein Gefühl von Exklusivität und Tiefe vermitteln. Es zeigt, dass hinter einem Piece mehr steckt als nur Stoff und Faden – es gibt eine Geschichte, eine Mathematik und eine Kunst.
Die Verbindung zur Natur
Fibonacci in der natürlichen Welt
Die Fibonacci-Sequenz und das goldene Verhältnis sind in der Natur allgegenwärtig: von der Anordnung der Blätter an Pflanzen bis zur Form von Galaxien. Durch die Einbindung dieses Musters in Streetwear-Kleidung kann ein Gefühl der Verbindung zur Natur entstehen.
Fazit: Die Symbiose von Mathematik und Mode
Streetwear und Fibonacci mögen auf den ersten Blick nicht viel gemeinsam haben, aber bei näherem Hinsehen gibt es faszinierende Überschneidungen. Das nächste Mal, wenn Sie Ihr Lieblingsoutfit im anziehen, denken Sie daran, wie Mathematik und Mode sich verbinden können, um Kunstwerke zu schaffen.

